BÀI 3. HÀM SỐ MŨ – HÀM SỐ LÔGARIT
⏳ Thời gian còn lại: 15:00
Câu 1. Tập xác định của hàm số \(y=2024^{\sqrt{x-3}}\) là:
Điều kiện: \(x-3\ge0 \Rightarrow x\ge3\).
Câu 2. Tập xác định của \(y=\log_{0,5}(6-2x)\) là:
Điều kiện: \(6-2x>0 \Rightarrow x<3.\)
Câu 3. Tập xác định \(y=\log_5(x^2-2x-3)\) là:
\(x^2-2x-3=(x-3)(x+1)>0\Rightarrow x<-1\) hoặc \(x>3.\)
Câu 4. Tập xác định \(y=\log\frac{1}{6-x}\)
Điều kiện: \(6-x>0 \Rightarrow x<6.\)
Câu 5. Tập xác định \(y=9^{\sqrt{x}}+\ln(8-2x)\)
Điều kiện: \(x\ge0\) và \(8-2x>0\Rightarrow x<4\Rightarrow[0;4).\)
Câu 6. Tìm m để \(y=\ln(x^2+mx+1)\) xác định ∀x∈ℝ
Để \(x^2+mx+1>0\) ∀x ⇒ Δ<0 ⇒ m^2-4<0 ⇒ -2<m<2.
Câu 7. Hàm số nào nghịch biến trên ℝ?
Cơ số <1 ⇒ nghịch biến ⇒ \(3/7<1.\)
Câu 8. Mệnh đề nào sai?
\(\ln x\) đồng biến ⇒ C sai.
Câu 9. Đồ thị hình dưới là của hàm nào?
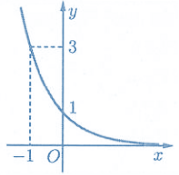
Đồ thị đi xuống ⇒ cơ số<1 ⇒ chọn \( (1/3)^x.\)
Câu 10. Quan hệ a,b đúng?
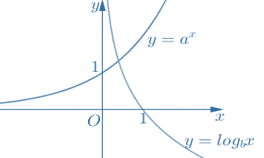
Đồ thị mũ đi lên ⇒ a>1; log đi xuống ⇒ b<1 ⇒ C.
