BÀI 3. HÀM SỐ LIÊN TỤC
⏳ Thời gian còn lại: 15:00
Câu 1. Hàm số y = f(x) có đồ thị dưới đây gián đoạn tại điểm có hoành độ bằng bao nhiêu? (Hình)
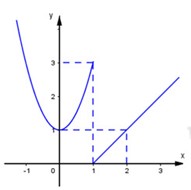
Quan sát đồ thị: có một điểm nhảy tại x = 1 nên hàm gián đoạn tại x = 1.
Câu 2. Cho hàm số \(f(x)=\left\{ \begin{array}{*{35}{l}}
\frac{{{x}^{2}}-6x+5}{{{x}^{2}}-1}\,\,\,\,\text{khi}\,\,\,\,x\ne 1 \\
a+2\,\,\,\,\text{khi}\,\,\,\,x=1 \\
\end{array} \right.\). Tìm \(a\) để hàm số \(y = f(x)\) liên tục tại \(x = 1\).
Giới hạn khi x→1: (x-5)/(x+1) tại x=1 = -2. Vậy a+2 = -2 → a = -4.
Câu 3. Cho hàm số \(f(x)=\begin{cases}x+2a \,\,\,\,\text{khi}\,\,\,\, x<0\\ x^{2}+x+1 \,\,\,\,\text{khi}\,\,\,\, x\geq 0\end{cases}\). Tìm \(a\) để hàm số \(y = f(x)\) liên tục tại \(x = 0\).
Giới hạn trái tại 0: 2a. Giới hạn phải tại 0: 1. Để liên tục: 2a=1 → a=1/2.
Câu 4. Cho hàm số \(f(x)=\begin{cases}3x-5\,\,\,khi\,\,\,x\le-2\\ax-1\,\,\,khi\,\,\,x>-2\end{cases}\). Tìm \(a\) để hàm số \(y = f(x)\) liên tục trên ℝ.
Giới hạn trái và giá trị tại -2: 3(-2)-5=-11. Giới hạn phải: a(-2)-1 = -2a-1. Bằng nhau → -2a-1=-11 → a=5.
Câu 5. Cho hàm số \(f(x)=\frac{x^{2}+1}{x^{2}+5x+6}\). Hàm số y = f(x) liên tục trên các khoảng nào sau đây?
Mẫu = (x+2)(x+3) → điểm không xác định x=-2,-3. Trên (-2,+∞) không có điểm kỳ dị nên liên tục.
Câu 6. Cho hàm số \(f(x)=\frac{5x-7}{x^2-9}\). Khẳng định nào sau đây đúng?
Mẫu = (x-3)(x+3). Hàm không xác định tại x=±3. Khoảng (-3,3) không chứa ±3, nên liên tục ở đó.
Câu 7. Cho hàm số \(f(x)=\sqrt{2x-6}\). Khẳng định nào sau đây sai?
Hàm chỉ xác định với x≥3 ⇒ không liên tục trên R. Vì vậy A sai.
Câu 8. Cho hai hàm số \(y = f(x)\) và \(y = g(x)\) liên tục tại điểm \(x_0\). Khẳng định nào sau đây sai?
Tỉ lệ chỉ liên tục khi g(x0)≠0. Vì đề không nêu điều kiện nên khẳng định D sai.
Câu 9. Cho hàm số \(f\left( x \right)=\frac{3x-1}{{{x}^{2}}-7x+12}\). Khẳng định nào sau đây đúng?
Mẫu = (x-3)(x-4). Hàm không xác định tại 3 và 4. Tại x=5 mẫu ≠0 nên liên tục.
Câu 10. Hàm số nào sau đây không liên tục tại \(x = 0\)?
1/x không xác định tại x=0 → không liên tục ở đó.
