BÀI 4. HÀM SỐ LƯỢNG GIÁC VÀ ĐỒ THỊ
⏳ Thời gian còn lại: 15:00
Câu 1. Tập xác định của hàm số \(y=\cos2x\) là:
Hàm cosine xác định trên mọi số thực nên tập xác định là \(\mathbb{R}\).
Câu 2. Tập xác định của hàm số \(y=\dfrac{\sin x}{\cos(x+\pi)}\) là:
Mẫu số \(\cos(x+\pi)=0\) khi \(x+\pi=\tfrac{\pi}{2}+k\pi\Rightarrow x=-\tfrac{\pi}{2}+k\pi\). Vậy tập xác định là \(\mathbb{R}\setminus\{ -\tfrac{\pi}{2}+k\pi\}\).
Câu 3. Tập xác định của hàm số \(y=\tan2x\) là:
\(\tan2x\) không xác định khi \(\cos2x=0\Rightarrow2x=\tfrac{\pi}{2}+k\pi\Rightarrow x=\tfrac{\pi}{4}+\tfrac{k\pi}{2}\). Vậy loại các điểm đó: đáp án D.
Câu 4. Tập xác định của hàm số \(y=\cot\big(2x-\tfrac{\pi}{3}\big)\) là:
\(\cot u\) không xác định khi \(\sin u=0\). Với \(u=2x-\tfrac{\pi}{3}\) ta có \(2x-\tfrac{\pi}{3}=k\pi\Rightarrow x=\tfrac{\pi}{6}+\tfrac{k\pi}{2}\). Đáp án A.
Câu 5. Tìm \(m\) để hàm số \(y=\dfrac{2}{\sin x-m}\) xác định trên \(\mathbb{R}\).
Để \(\sin x-m\ne0\) với mọi \(x\) cần \(m\) không thuộc đoạn giá trị của \(\sin x\), tức là \(m\notin[-1,1]\). Vậy đáp án A.
Câu 6. Tập giá trị của hàm số \(y=2-\sin x\) là:
Vì \(\sin x\in[-1,1]\) nên \(2-\sin x\in[2-1,2+1]=[1,3]\). Đáp án C.
Câu 7. Trong các hàm số sau đây, hàm số nào là hàm số tuần hoàn?
Chỉ \(\sin x\) là tuần hoàn với chu kỳ \(2\pi\). Các hàm còn lại không tuần hoàn. Đáp án A.
Câu 8. Mệnh đề nào sau đây là mệnh đề sai?
B sai vì \(\cos x\) có chu kỳ \(2\pi\) (không phải \(\pi\)). \(\tan x\) đúng là có chu kỳ \(\pi\). Đáp án B.
Câu 9. Hàm số nào sau đây là hàm số chẵn?
\(\cos(-x)=\cos x\) nên \(\cos x\) là hàm chẵn. Đáp án B.
Câu 10. Hình vẽ sau là đồ thị của hàm số nào?
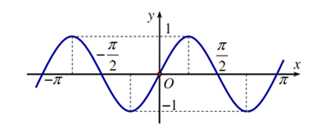

Đồ thị bắt đầu tại điểm (0,1) và có dạng dịch chuyển của \(\cos x\), nên đáp án B: \(y=\cos x\).
