BÀI 3. NHỊ THỨC NEWTON
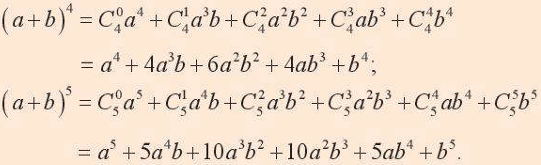
CÁC VÍ DỤ MINH HỌA
① $(x + y)^5$
② $\left(\sqrt{x} + \dfrac{1}{x}\right)^4$
Lời giải
Áp dụng khai triển nhị thức Newton, ta có:
① $(x + y)^5 = C_0^5x^5 + C_1^5x^4y + C_2^5x^3y^2 + C_3^5x^2y^3 + C_4^5xy^4 + C_5^5y^5$
$= x^5 + 5x^4y + 10x^3y^2 + 10x^2y^3 + 5xy^4 + y^5.$
② $\left(\sqrt{x} + \dfrac{1}{x}\right)^4 = C_0^4(\sqrt{x})^4 + C_1^4(\sqrt{x})^3\dfrac{1}{x} + C_2^4(\sqrt{x})^2\left(\dfrac{1}{x}\right)^2 + C_3^4\sqrt{x}\left(\dfrac{1}{x}\right)^3 + C_4^4\left(\dfrac{1}{x}\right)^4.$
$= x^2 + 4\sqrt{x} + \dfrac{6}{x} + \dfrac{4}{x^{3/2}} + \dfrac{1}{x^2}$ (với $x>0$).
① $(2x^3 - 1)^5$
② $\left(y - \dfrac{3}{y}\right)^4$
Lời giải
① $(2x^3 - 1)^5 = C_0^5(2x^3)^5 + C_1^5(2x^3)^4(-1) + C_2^5(2x^3)^3(-1)^2 + C_3^5(2x^3)^2(-1)^3 + C_4^5(2x^3)(-1)^4 + C_5^5(-1)^5$
$= 32x^{15} - 80x^{12} + 80x^9 - 40x^6 + 10x^3 - 1.$
② $\left(y - \dfrac{3}{y}\right)^4 = C_0^4y^4 + C_1^4y^3\left(-\dfrac{3}{y}\right) + C_2^4y^2\left(-\dfrac{3}{y}\right)^2 + C_3^4y\left(-\dfrac{3}{y}\right)^3 + C_4^4\left(-\dfrac{3}{y}\right)^4$
$= y^4 - 12y^2 + 54 - \dfrac{108}{y^2} + \dfrac{81}{y^4}.$
