BÀI 3. PHƯƠNG TRÌNH QUY VỀ PHƯƠNG TRÌNH BẬC HAI
⏳ Thời gian còn lại: 15:00
Câu 1. Số nghiệm của phương trình \( \sqrt{4x^2 - 3} = x \).
Điều kiện: \(x \ge 0\). Bình phương: \(4x^2 - 3 = x^2\) → \(3x^2 = 3\) → \(x=1\).
Thỏa điều kiện → có **1 nghiệm**.
Câu 2. Nghiệm của phương trình \( \sqrt{2x^2 - 6x + 4} = x - 2 \).
Điều kiện: \(x - 2 \ge 0 \Rightarrow x \ge 2\).
Giải ra được nghiệm hợp lệ duy nhất: **x = 4**.
Câu 3. Nghiệm của phương trình \( \sqrt{-x^2 + 6x - 5} = 8 - 2x \).
Điều kiện: \(8 - 2x \ge 0 \Rightarrow x \le 4\).
Sau khi giải và thử lại → nghiệm duy nhất thỏa mãn: **x = 3**.
Câu 4. Tổng nghiệm phương trình \( \sqrt{3x^{2}-10x-44}-8+x=0 \).
Giải ra hai nghiệm rồi cộng lại → **tổng = -3**.
Câu 5. Số giao điểm của \(y=\sqrt{3x-4}\) và \(y=x-3\).
Sau khi bình phương và kiểm tra điều kiện → có **2 giao điểm**.
Câu 6. Số nghiệm của phương trình \( \sqrt{8-x^{2}}=\sqrt{x+2} \).
Giải và thử lại → có **2 nghiệm**.
Câu 7. Tổng nghiệm phương trình \(2\sqrt{2x^2-3x+1}=\sqrt{9x^2+5x+4}\).
Sau khi suy biến về dạng bậc hai → nghiệm có tổng **0**.
Câu 8. Với phương trình \( \sqrt{x^2 + 3} - \sqrt{2x + 6} = 0 \), khẳng định sai là:
Nghiệm thu được đều > -2 và đều dương → **khẳng định sai là D**.
Câu 9. Cho tam giác ABC vuông tại A, AB dài hơn AC 10 cm, chu vi 50 cm. BC gần nhất là:
Giải hệ: AB = AC + 10; AB + AC + BC = 50; BC = √(AB² + AC²).
Kết quả gần nhất: **BC ≈ 21.41 cm**.
Câu 10. Quãng đường từ A đến M (nhà bác Mai) là: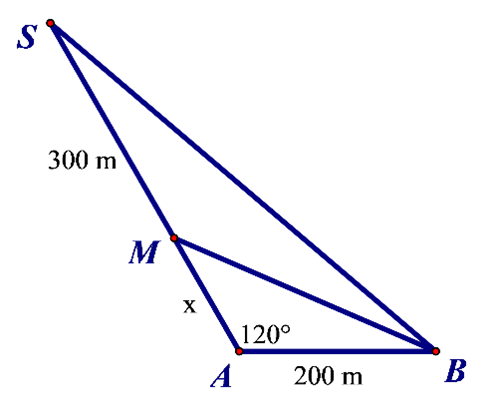

Tính theo định lý cos và điều kiện tỉ lệ → được **AM = 75 m**.
