BÀI 1 – DẤU CỦA TAM THỨC BẬC HAI
⏳ Thời gian còn lại: 15:00
Câu 1. Bảng xét dấu của tam thức \(f(x)=x^2+2x+1\) là:
\(f(x)=x^2+2x+1=(x+1)^2\) có nghiệm kép x = -1 và hệ số a = 1 > 0.
→ Tam thức không âm và bằng 0 tại x = -1.
→ Bảng xét dấu đúng là A.
Câu 2. Tìm các giá trị của m để \(f(x)=(m+2)x^2-3mx+1\) là tam thức bậc hai.
Để là tam thức bậc hai thì hệ số của \(x^2\) phải ≠ 0:
\[
m+2 \ne 0 \Rightarrow m \ne -2.
\]
→ Đáp án đúng: B.
Câu 3. Tìm m để \(f(x)=x^2+4x+m+3\) luôn dương.
Ta xét tam thức có a = 1 > 0.
Để luôn dương thì:
• ∆ < 0
• Hoặc ∆ = 0 nhưng giá trị tại đỉnh > 0.
Ta tính:
\[
\Delta = 4^2 - 4(1)(m+3) = 16 - 4m - 12 = 4 - 4m
\]
Muốn f(x) luôn dương ⇒ ∆ < 0:
\[
4 - 4m < 0 \Rightarrow m > 1.
\]
→ Đáp án đúng: C.
Câu 4. Cho đồ thị tam thức bậc hai sau:
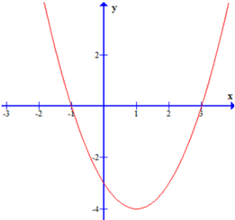
Bảng biến thiên tương ứng là:
Đồ thị mở xuống (a < 0), đạt cực đại.
→ Chỉ bảng biến thiên C phù hợp.
→ Đáp án đúng: C.
Câu 5. Biểu thức nào sau đây là tam thức bậc hai?
Tam thức bậc hai phải có dạng:
\[
ax^2 + bx + c, \quad a \ne 0
\]
Chỉ phương án B là tam thức bậc hai.
→ Đáp án đúng: B.
Câu 6. Tam thức nào nhận giá trị âm với mọi x < 1?
Ta xét từng hàm.
Hàm D: \(-x^2+5x-4\) mở xuống, nghiệm là 1 và 4.
→ Với x < 1, ta luôn có f(x) < 0.
→ Đáp án đúng: D.
Câu 7. Tìm x để \(y=-x^2-3x+4\) nhận giá trị âm.
Nghiệm tam thức:
\[
-x^2-3x+4=0 \Rightarrow x=-4,\; x=1.
\]
Vì hệ số a < 0 (mở xuống) → âm khi nằm ngoài khoảng nghiệm.
→ f(x) < 0 khi \(-4 < x < 1\)
→ Đáp án đúng: C.
Câu 8. Biệt thức của \(f(x)=-x^2-4x-6\) là:
Ta có:
\[
\Delta = b^2 - 4ac = (-4)^2 - 4(-1)(-6) =16 - 24 = -8
\]
\[
\Delta' = a\Delta/4 = (-1)(-8)/4 = -2
\]
→ Đáp án đúng: D.
Câu 9. Tập nghiệm để \(x^2-6x+8 \le 0\) là:
Nghiệm tam thức:
\[
x^2-6x+8=0 \Rightarrow x=2;\; x=4
\]
Vì a > 0 → ≤ 0 trong khoảng giữa hai nghiệm:
→ [2;4]
→ Đáp án đúng: C.
Câu 10. Tìm m để \(f(x)=x^2-(m+2)x+8m+1\) đổi dấu.
Tam thức đổi dấu ⇔ có hai nghiệm phân biệt.
Điều kiện:
\[
\Delta > 0
\]
\[
\Delta = (m+2)^2 - 4(1)(8m+1)
\]
\[
= m^2+4m+4 - 32m - 4 = m^2 - 28m
\]
\[
m(m-28) > 0 \Rightarrow m < 0 \text{ hoặc } m > 28
\]
→ Đáp án đúng: C.
