Trắc nghiệm: Các số đặc trưng đo mức độ phân tán của mẫu số liệu – 10 câu (Có Timer)

BÀI 4. CÁC SỐ ĐẶC TRƯNG ĐO MỨC ĐỘ PHÂN TÁN CỦA MẪU SỐ LIỆU

⏳ Thời gian còn lại: 15:00

Câu 1. Cho một mẫu số liệu được sắp xếp theo thứ tự không giảm như sau \(x_1 \le x_2 \le \dots \le x_n\). Khi đó khoảng biến thiên của mẫu số liệu đã cho bằng:

A. \(x_n - x_1\) B. \(x_1 - x_n\) C. \(\dfrac{x_n - x_1}{2}\) D. \(\dfrac{x_1 - x_n}{2}\)

Đáp án đúng: A. Giải thích: Khoảng biến thiên \(R\) xác định sự chênh lệch giữa giá trị lớn nhất và giá trị nhỏ nhất trong mẫu, do đó \[ R = x_n - x_1. \]

Câu 2. Điểm kiểm tra giữa học kì I của tổ 1: 6; 7; 7; 5; 8; 6; 9; 9; 8; 6. Khoảng biến thiên của mẫu số liệu này bằng:

A. 5 B. 4 C. 3 D. 2

Đáp án đúng: B. Giải: Sắp xếp ta có giá trị nhỏ nhất \(=5\), lớn nhất \(=9\). Do đó \[ R = 9 - 5 = 4. \]

Câu 3. Có 100 học sinh dự kì thi (thang điểm 20). Bảng tần số cho bởi hình dưới:

A. 3,69 B. 3,71 C. 3,95 D. 3,96

Đáp án đúng: D. Bảng tần số (theo ảnh): điểm 9→19 với tần số tương ứng: \(1,1,3,5,8,13,19,24,14,10,2\) (tổng \(N=100\)). Tính trung bình: \[ \bar x = \dfrac{\sum x_i n_i}{N} = \frac{9\cdot1+10\cdot1+\dots+19\cdot2}{100}=15{,}23. \] Tính phương sai (phương sai dân số, chia cho \(N\)): \[ \sigma^2 = \dfrac{\sum x_i^2 n_i}{N} - \bar x^2. \] Tính cụ thể: \(\dfrac{\sum x_i^2 n_i}{N} \approx (15{,}23)^2 + 3{,}9571\), suy ra \(\sigma^2 \approx 3{,}9571\), làm tròn đến hàng phần trăm: \(3{,}96\). Vậy chọn D.

Câu 4. Độ lệch chuẩn là gì?

A. Độ lệch chuẩn là bình phương của phương sai. B. Độ lệch chuẩn là một nửa của phương sai. C. Độ lệch chuẩn là căn bậc hai của phương sai. D. Độ lệch chuẩn là căn bậc ba của phương sai.

Đáp án đúng: C. Giải thích: Độ lệch chuẩn \(S\) (hoặc \(\sigma\)) được định nghĩa là căn bậc hai của phương sai: \[ S = \sqrt{\text{phương sai}}. \]

Câu 5. Số tiền nước (nghìn đồng) của 5 hộ: 56; 45; 103; 239; 125. Độ lệch chuẩn (làm tròn đến hàng phần trăm) gần bằng:

A. 69,22 B. 69,25 C. 69,27 D. 69,29

Đáp án đúng: C. Giải: Dùng công thức độ lệch chuẩn dân số (chia cho \(n\)): Dữ liệu: \(56,45,103,239,125\). Trung bình: \(\bar x = \dfrac{56+45+103+239+125}{5}=113.6\). Phương sai (dân số): \[ \sigma^2=\frac{1}{5}\sum (x_i-\bar x)^2 \approx 4800{,}9\quad(\text{tính nội suy}), \] suy ra \(\sigma\approx 69{,}269\). Làm tròn đến hàng phần trăm: \(69{,}27\).

Câu 6. Chiều cao (cm) của 10 học sinh: 154;160;155;162;165;162;155;160;165;162. Khoảng tứ phân vị (IQR) bằng:

A. 5 B. 6 C. 7 D. 8

Đáp án đúng: C. Giải: Sắp xếp tăng dần: \(154,155,155,160,160,162,162,162,165,165\). Vì \(n=10\) (chẵn), ta chia làm hai nửa: phần dưới 5 giá trị \(154,155,155,160,160\) → \(Q_1 = 155\). Phần trên 5 giá trị \(162,162,162,165,165\) → \(Q_3 = 162\). Do đó \(IQR = Q_3 - Q_1 = 162 - 155 = 7.\)

Câu 7. Cho mẫu: 10; 8; 6; 8; 9; 8; 7; 6; 9; 9; 7. Khoảng tứ phân vị của mẫu bằng:

A. 1 B. 3 C. 4 D. 2

Đáp án đúng: D. Giải: Sắp xếp: \(6,6,7,7,8,8,8,9,9,9,10\) (n=11). Với n lẻ: trung vị là phần tử thứ 6 (ở đây là \(8\)). Phần dưới: \(6,6,7,7,8\) → \(Q_1=7\). Phần trên: \(8,9,9,9,10\) → \(Q_3=9\). IQR = \(9-7=2\).

Câu 8. Sản lượng lúa (tạ) của 40 thửa ruộng được cho bảng:

A. 1,23 B. 1,24 C. 1,25 D. 1,26

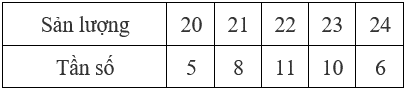
Đáp án đúng: B. Bảng tần số (theo ảnh): sản lượng \(20,21,22,23,24\) với tần số \(5,8,11,10,6\) (tổng \(N=40\)). Tính trung bình: \[ \bar x = \frac{20\cdot5+21\cdot8+22\cdot11+23\cdot10+24\cdot6}{40}=22{,}2. \] Phương sai dân số: \[ \sigma^2=\frac{\sum (x_i-\bar x)^2 n_i}{N}\approx 1{,}540\quad\Rightarrow\quad \sigma\approx 1{,}24097. \] Làm tròn đến hàng phần trăm: \(1{,}24\).

Câu 9. Mệnh đề nào sau đây **sai**?

A. Khoảng biến thiên đặc trưng cho độ phân tán của toàn bộ mẫu số liệu. B. Khoảng tứ phân vị đặc trưng cho độ phân tán của một nửa các số liệu, có giá trị thuộc đoạn từ \(Q_1\) đến \(Q_3\) trong mẫu. C. Khoảng tứ phân vị bị ảnh hưởng bởi các giá trị rất lớn hoặc rất bé trong mẫu. D. Khoảng tứ phân vị được dùng để xác định các giá trị ngoại lệ trong mẫu.

Đáp án đúng (câu sai): C. Giải: - A: đúng (khoảng biến thiên dùng toàn dãy: max − min). - B: đúng (IQR đo độ phân tán của phần giữa 50% số liệu, thuộc đoạn từ \(Q_1\) đến \(Q_3\)). - C: sai — khoảng tứ phân vị **không** bị ảnh hưởng mạnh bởi các giá trị rất lớn hoặc rất nhỏ (đó là ưu điểm của IQR). - D: đúng — IQR thường dùng để xác định ngoại lệ (theo quy tắc 1.5·IQR).

Câu 10. Mệnh đề nào sau đây **đúng**?

A. Nếu các giá trị của mẫu càng tập trung quanh giá trị trung bình thì độ lệch chuẩn càng lớn. B. Khoảng biến thiên chỉ sử dụng thông tin của giá trị lớn nhất và bé nhất, bỏ qua thông tin của các giá trị còn lại. C. Khoảng tứ phân vị có sử dụng thông tin của giá trị lớn nhất và bé nhất. D. Các số đo độ phân tán có thể bằng 0.

Đáp án đúng: B. Giải: - A: sai — nếu các giá trị tập trung quanh trung bình thì độ lệch chuẩn **nhỏ** (không lớn). - B: đúng — khoảng biến thiên \(R\) chỉ tính \(R = \text{max} - \text{min}\), tức chỉ dùng giá trị lớn nhất và nhỏ nhất. - C: sai — khoảng tứ phân vị không phụ thuộc trực tiếp vào giá trị lớn nhất/nhỏ nhất (nó dùng phần giữa của mẫu). - D: sai/vô vị — các số đo độ phân tán có thể **bằng 0** (nếu tất cả giá trị bằng nhau) — nhưng trong các tài liệu tương tự, phương án B thường được chọn là mô tả đặc trưng của khoảng biến thiên; mình giữ đáp án theo nguồn câu hỏi gốc là B.