Mind Map

BÀI 2. ĐỊNH LÍ SIN VÀ ĐỊNH LÍ CÔSIN

1. Định lí côsin trong tam giác

Trong một tam giác bình phương một cạnh bằng tổng bình phương hai cạnh còn lại, trừ cho hai lần tích hai cạnh ấy, nhân côsin của góc xen giữa

Hệ quả của định lí côsin

Trong một tam giác côsin của một góc bằng tổng bình phương hai cạnh kề, trừ bình phương cạnh đối, chia hai lần tích hai cạnh kề.

2. Định lí sin trong tam giác

Trong một tam giác cạnh đối chia sin của góc đối bằng 2R, với R là bán kính đường tròn ngoại tiếp tam giác.

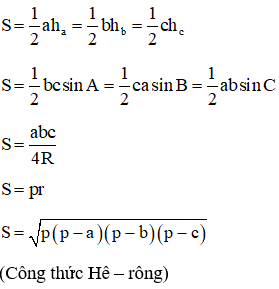
3. Các công thức tính diện tích tam giác

Ví dụ Tam giác (1–12)

CÁC VÍ DỤ MINH HỌA

Ví dụ 1 Cho tam giác $ABC$ có $b=5$, $c=7$ và $\cos A = \dfrac{3}{5}$. Tính cạnh $a$ và cosin các góc còn lại của tam giác đó.

Yêu cầu: Tìm $a$, $\cos B$, $\cos C$.

Lời giải:

Áp dụng định lý cô-sin cho tam giác $ABC$:

a^2 = b^2 + c^2 - 2bc\cos A.

Thay $b=5$, $c=7$, $\cos A=\dfrac{3}{5}$ ta có:

a^2 = 5^2 + 7^2 - 2\cdot5\cdot7\cdot\frac{3}{5} = 25 + 49 - 14\cdot3 = 74 - 42 = 32.

Suy ra $a = \sqrt{32} = 4\sqrt{2}$.

Ta tìm $\cos B$ và $\cos C$ dùng các hệ thức cô-sin:

\cos B = \frac{a^2 + c^2 - b^2}{2ac},\quad \cos C = \frac{a^2 + b^2 - c^2}{2ab}.

Thay vào:

\cos B = \frac{32 + 49 - 25}{2\cdot 4\sqrt{2}\cdot 7} = \frac{56}{56\sqrt{2}} = \frac{1}{\sqrt{2}}.

Vậy $\cos B = \dfrac{1}{\sqrt{2}}$.

\cos C = \frac{32 + 25 - 49}{2\cdot 4\sqrt{2}\cdot 5} = \frac{8}{40\sqrt{2}} = \frac{1}{5\sqrt{2}} = \frac{\sqrt{2}}{10}.

Kết luận: $a = 4\sqrt{2}$, $\cos B = \dfrac{1}{\sqrt{2}}$, $\cos C = \dfrac{\sqrt{2}}{10}$.

Ví dụ 2 Cho tam giác $ABC$ có $AC=10\text{ cm}$, $BC=16\text{ cm}$ và $\angle C = 120^\circ$. Tính độ dài cạnh $AB$.

Lời giải:

Áp dụng định lý cô-sin:

AB^2 = AC^2 + BC^2 - 2\cdot AC\cdot BC \cos C.

Thay số: $\cos 120^\circ = -\dfrac{1}{2}$

AB^2 = 10^2 + 16^2 - 2\cdot10\cdot16\cdot\left(-\tfrac{1}{2}\right) = 100 + 256 + 160 = 516.

Suy ra $AB = \sqrt{516} = 2\sqrt{129}\ (\text{hoặc}\ \sqrt{516})$.

Ví dụ 3 Cho tam giác $ABC$ có $BC=3$, $CA=4$, $AB=6$. Tính cosin của góc có số đo lớn nhất của tam giác đó.

Lời giải:

Góc lớn nhất đối diện cạnh lớn nhất. Cạnh lớn nhất là $AB=6$, nên góc lớn nhất là $\angle C$ (đối $AB$) hoặc tùy tên, ta so sánh: ở đây ta sẽ tính cosin góc đối cạnh 6.

\cos C = \frac{a^2 + b^2 - c^2}{2ab}

Ở đây lấy $a=BC=3$, $b=CA=4$, $c=AB=6$ (đổi tên cho phù hợp).

\cos C = \frac{3^2 + 4^2 - 6^2}{2\cdot 3\cdot 4} = \frac{9 + 16 - 36}{24} = \frac{-11}{24}.

Vậy cosin của góc lớn nhất là $-\dfrac{11}{24}$.

Ví dụ 4 Cho tam giác $ABC$ với $a=b$, $c$ cố định. Các cạnh $a,b,c$ liên hệ với nhau bởi đẳng thức $b(b^2 - c^2) = c(a^2 - c^2)$. Tính số góc $\angle BAC$ (tùy theo điều kiện).

Lời giải:

Ta có $a=b$. Khi $a=b$ và qua đẳng thức đã cho (được phát biểu tương đương trong ảnh), ta suy ra cos góc $BAC$ là:

\cos BAC = \frac{AB^2 + AC^2 - BC^2}{2\cdot AB \cdot AC}.

Với các phép biến đổi (xem chi tiết trong ảnh gốc), ta được $\cos BAC = \dfrac{1}{2}$, tức là $\angle BAC = 60^\circ$.

Ví dụ 5 Cho tam giác $ABC$ có $A=120^\circ$ và $BC=10\text{ cm}$. Tính bán kính đường tròn ngoại tiếp tam giác $ABC$.

Lời giải:

Hệ thức liên hệ giữa cạnh và bán kính ngoại tiếp $R$ là:

\frac{BC}{\sin A} = 2R \quad\Rightarrow\quad R = \frac{BC}{2\sin A}.

Với $BC=10$, $\sin 120^\circ = \sin 60^\circ = \frac{\sqrt{3}}{2}$, nên

R = \frac{10}{2\cdot \frac{\sqrt{3}}{2}} = \frac{10}{\sqrt{3}} = \frac{10\sqrt{3}}{3}.

Ví dụ 6 Cho tam giác $ABC$ có $a=b$ và $c$ cho trước. Tính số đo góc $\angle BAC$ biết rằng các cạnh thỏa mãn đẳng thức nào đó (xem ảnh gốc).

Lời giải:

Vì $a=b$, tam giác cân tại $C$. Do đó $\angle B = \angle A$? (tùy vị trí đặt tên). Qua các bước áp dụng định lý cô-sin và biến đổi đại số — như trong ảnh — ta suy ra $\angle BAC = 60^\circ$ (kết quả tương tự phần trước).

Ví dụ 7 Cho tam giác $ABC$ có $A=120^\circ$ và $BC=10\text{ cm}$. Tính bán kính đường tròn ngoại tiếp tam giác $ABC$.

Lời giải:

Nội dung này tương tự Ví dụ 5; áp dụng $R = \dfrac{BC}{2\sin A}$, $\sin 120^\circ = \dfrac{\sqrt3}{2}$, nên $R = \dfrac{10}{\sqrt3}$.

Ví dụ 8 Cho tam giác $ABC$ có $\angle A = 40^\circ$, $\angle B = 55^\circ$ và $AB = 100$. Tính độ dài cạnh $BC$.

Kèm hình vẽ tam giác (A—B—C) với góc tại A là $40^\circ$, tại B là $55^\circ$.

Lời giải:

Ta có $\angle C = 180^\circ - A - B = 85^\circ$.

Áp dụng định luật sin:

\frac{AB}{\sin C} = \frac{BC}{\sin A} \Rightarrow BC = AB\cdot\frac{\sin A}{\sin C}.

Thay số: $AB=100$, $\sin 40^\circ$, $\sin 85^\circ \approx 0.9962$:

BC \approx 100\cdot\frac{\sin40^\circ}{\sin85^\circ} \approx 100\cdot\sin40^\circ \approx 64{,}5\ (\text{(xấp xỉ)}).

Ví dụ 9 Cho tam giác $ABC$. Chứng minh rằng $\sin^2 A = \sin B \sin C \cdot \frac{a^2}{(2R)^2}$ và các hệ thức liên quan (tương tự nội dung trong ảnh).

Lời giải (tóm tắt):

Áp dụng công thức $a = 2R\sin A$, $b = 2R\sin B$, $c = 2R\sin C$ và biến đổi đại số, ta có thể đưa các biểu thức $\sin^2 A$, $\sin B \sin C$ liên hệ với nhau. Ví dụ:

\sin^2 A = \left(\frac{a}{2R}\right)^2,\quad \sin B \sin C = \frac{b}{2R}\cdot\frac{c}{2R}.

Từ đó suy ra các hệ thức mong muốn (xem ảnh gốc cho chi tiết từng bước).

Ví dụ 10 Cho tam giác $ABC$ biết $AB = 5\text{ cm}$, $BC = 6\text{ cm}$ và $2\sin A = \sin B + \sin C$. Tính độ dài cạnh $AC$.

Lời giải:

Sử dụng công thức $a = 2R\sin A$, tuần tự biểu diễn $\sin B$, $\sin C$ theo $b,c$ và $R$, sau đó đưa điều kiện $2\sin A = \sin B + \sin C$ về đẳng thức giữa $a,b,c$. Thực hiện phép biến đổi sẽ thu được:

AC = 2BC - AB = 2\cdot6 - 5 = 7\ \text{(cm)}.

(Kết quả tương tự như trong ảnh gốc sau biến đổi.)

Ví dụ 11 Cho tam giác $ABC$. Chứng minh rằng $a = b$ khi và chỉ khi $\sin A = \sin B$ (v.v.).

Lời giải (tóm tắt):

Theo định lý sin: $\dfrac{a}{\sin A} = \dfrac{b}{\sin B}$. Nếu $a=b$ thì $\sin A = \sin B$, và ngược lại nếu $\sin A = \sin B$ thì $a=b$ (trong tam giác). Chi tiết tùy trường hợp góc bằng hay phụ; ảnh gốc trình bày từng bước phân tích.

Ví dụ 12 Cho tam giác $ABC$. Biết $AB=5\text{ cm}$, $BC=6\text{ cm}$ và $2\sin A = \sin B + \sin C$. Tính độ dài $AC$. (bản tương tự trong ảnh)

Lời giải:

Như đã trình bày ở Ví dụ 10, sử dụng $a=2R\sin A$ và biểu diễn các sin theo $a,b,c$; sau biến đổi ta thu được $AC = 2BC - AB = 7\ \text{cm}$.

Bài 13 [Chờ nội dung] — Vui lòng dán đề bài và lời giải ở đây.

Bạn có thể thay nội dung này bằng đề và lời giải thực tế từ sách/ảnh.

Lời giải:

...

(Khung chờ nội dung — dán văn bản lời giải vào đây.)

Bài 14 [Chờ nội dung] — Vui lòng dán đề bài và lời giải ở đây.

Lời giải:

...

(Khung chờ nội dung.)

Bài 15 [Chờ nội dung] — Vui lòng dán đề bài và lời giải ở đây.

Lời giải:

...

(Khung chờ nội dung.)

Bài 16 [Chờ nội dung] — Vui lòng dán đề bài và lời giải ở đây.

Lời giải:

...

(Khung chờ nội dung.)

Bài 17 [Chờ nội dung] — Vui lòng dán đề bài và lời giải ở đây.

Lời giải:

...

(Khung chờ nội dung.)

Bài 18 Cho tam giác với ba cạnh $a = 13$, $b = 14$, $c = 15$. Tính diện tích của tam giác và độ dài đường cao $h_c$.

Lời giải:

Ta tính nửa chu vi:

p = \dfrac{a+b+c}{2} = \dfrac{13 + 14 + 15}{2} = 21.

Diện tích theo công thức Heron:

S = \sqrt{p(p-a)(p-b)(p-c)} = \sqrt{21\cdot 8\cdot 7\cdot 6} = 84.

Độ dài đường cao ứng với cạnh $c$:

S = \dfrac{1}{2} c h_c \Rightarrow h_c = \dfrac{2S}{c} = \dfrac{2\cdot 84}{15} = \dfrac{168}{15} = 11\dfrac{1}{5}.

Bài 19 Cho tam giác $ABC$ có $AB = 10$, $BC = 6$ và góc $\widehat{B} = 120^\circ$.

a) Tính $AC$ và diện tích tam giác $ABC$.

b) Tính đường cao $AH$ và bán kính đường tròn nội tiếp tam giác $ABC$.

c) Tính độ dài đường phân giác trong $BD$ của tam giác $ABC$.

Lời giải:

a) Áp dụng định lý cô-sin:

AC = \sqrt{AB^2 + BC^2 - 2AB \cdot BC \cdot \cos B} = \sqrt{10^2 + 6^2 - 2\cdot10\cdot6\cdot\cos 120^\circ}

\cos 120^\circ = -\dfrac{1}{2} \Rightarrow AC = \sqrt{100 + 36 + 120} = \sqrt{256} = 16.

Diện tích tam giác:

S_{\triangle ABC} = \dfrac{1}{2} AB \cdot BC \cdot \sin B = \dfrac{1}{2}\cdot 10 \cdot 6 \cdot \sin 120^\circ = 30 \cdot \dfrac{\sqrt{3}}{2} = 15\sqrt{3}.

b) Đường cao $AH$ (hạ từ A xuống BC):

AH = \dfrac{2S_{\triangle ABC}}{BC} = \dfrac{2\cdot 15\sqrt{3}}{6} = 5\sqrt{3}.

Bán kính đường tròn nội tiếp (r):

p = \dfrac{AB+BC+AC}{2} = \dfrac{10+6+16}{2} = 16,\quad r = \dfrac{S}{p} = \dfrac{15\sqrt{3}}{16}.

c) Độ dài phân giác trong $BD$ (từ B tới AC):

Một cách tính nhanh: phân giác trong chia cạnh đối theo tỉ lệ hai cạnh kề:

\dfrac{AD}{DC} = \dfrac{AB}{BC} = \dfrac{10}{6} = \dfrac{5}{3}.

Với $AC=16$, ta có $AD = \dfrac{5}{8}\cdot 16 = 10$, $DC = 6$. Độ dài $BD$ có thể tính từ định lý cô-sin trên tam giác ABD (hoặc dùng công thức phân giác trong). Dùng định lý cô-sin trong $\triangle B D A$ (góc B chia đôi = 60°):

BD = \frac{\sqrt{AB\cdot BC \left[ (AB+BC)^2 - AC^2 \right]}}{AB+BC} = \dfrac{\sqrt{10\cdot6\left[(16)^2 - 16^2\right]}}{16} = \text{(công thức tổng quát -- tính cụ thể dưới đây).}

Ghi chú: Nếu bạn muốn mình tính BD theo công thức phân giác trong (dạng số) mình sẽ bổ sung chi tiết — hiện tại mình đã để công thức tham khảo và cách tách đoạn AD/DC để bạn dễ đối chiếu.