BÀI 2. TẬP HỢP
1. Nhắc lại về tập hợp
a) Tập hợp
Ví dụ 1: Gọi A là tập hợp các số tự nhiên bé hơn 5
❑ Nhận xét:
✅ Các số 0; 1; 2; 3; 4 là các phần tử của tập hợp A
✅ Số 3 thuộc tập hợp A. Kí hiệu 3 ∊ A
✅ Số 6 không thuộc tập hợp A. Kí hiệu 6 ∉ A
✅ “Tập hợp” gọi tắt là “tập”
✅ Tập hợp không có phần tử nào gọi là tập rỗng. Kí hiệu ∅
❑ Chú ý:
✅ Tập hợp thường được kí hiệu: A, B, C,…
✅ Phần tử thường được kí hiệu: a, b, c,…
b) Cách xác định tập hợp
▪ Cách 1: Liệt kê các phần tử
Xét lại ví dụ 1: A = {0; 1; 2; 3; 4}
▪ Cách 2: Chỉ ra tính chất đặc trưng
Xét lại ví dụ 1: A = {x ∊ ℕ | x < 5}
❑ Chú ý:
✅ Nếu E là tập hợp hữu hạn thì số phần tử của tập hợp E kí hiệu là n(E).
2. Tập con và phần bù của hai tập hợp
a) Tập con
Nếu mọi phần tử của tập hợp A đều thuộc tập hợp B thì ta nói tập hợp A là tập con của tập hợp B. Kí hiệu là A ⊂ B
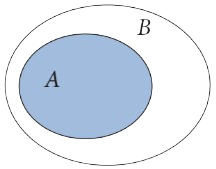
Ví dụ 2: Cho A = {1; 2} và B = {1; 2; 3}. Khi đó A ⊂ B
❑ Nhận xét
✅ A ⊂ A và ∅ ⊂ A với mọi tập hợp A
✅ Nếu A không phải là tập con của B thì ta kí hiệu A ⊄ B
b) Hai tập hợp bằng nhau
▪ Hai tập hợp A và B gọi là bằng nhau, kí hiệu A = B, nếu A ⊂ B và B ⊂ A.
Ví dụ 3: Cho A = {-2; -1; 0; 1; 2} và B = {x ∊ ℤ | |x| ≤ 2}. Khi đó A = B
3. Một số tập con của tập hợp số thực
Sau này ta thường sử dụng các tập con của tập số thực sau đây (a và b là các số thực, a<b)

Ví dụ 4: Tập hợp A = {x ∊ ℝ | x < 3} còn được viết là A = (-∞ ; 3)
